【資産形成・初心者向け】アインシュタインが人類最大の発明と評した『複利』とは

始めに

研修医

『複利』って何ですか？

Taka

複利は金利の計算方法の1つです。

複利効果についてはかのアインシュタインが『人類最大の発明』と称するほどの威力があります。

詳しく解説していきます。

皆さんは『利息』という言葉は聞き覚えがあるかと思います。

利息は金銭の貸し借りにおける対価として、金額や期間に比例して一定割合で支払われる金銭を指します。

ここまではイメージがつく方が大半と思いますが計算方法に『単利』と『複利』という計算方法があることまではご存じでしょうか。

この記事では複利とそれが生み出す効果について解説します。

既に知っているという方は読まなくてもいいですし、再度のInputのために一読頂いても良いと思います。

『単利』・『複利』とは

研修医

よくわかりません。。

Taka

確かにこれだけだとイメージしにくいと思いますので具体例を提示します。

①単利計算の例

元本100万円を年利１％で5年間運用した場合の例を示します。

単利の場合、5年後の利息受取額合計は50,000円です。

②複利計算の例

比較のためにこちらも元本100万円を年利１％で5年間運用した場合の例を示します。

さっきと異なる点は利息が元金に組み込まれる点です。

複利の場合、5年後の利息受取額合計は51,010円です。

単利の場合と比べて1010円の差が生まれることになります。

研修医

思ってたより少ないですね。。

Taka

まあ、5年間で計算したので。

あくまで複利計算の方がプラスになることを理解してほしかっただけです。

年数が増えるほど増す複利の威力

先ほどの結果を受けて同じく「1000円しか変わらないのか。。」と思った方も多いかと思います。

ただ、複利の威力は運用年数が長くなるほど威力を増してきます。

下記は金融庁のサイトを用いたシミュレーションになります。

月に5万円ずつを積み立て利率3％で運用したパターンです。

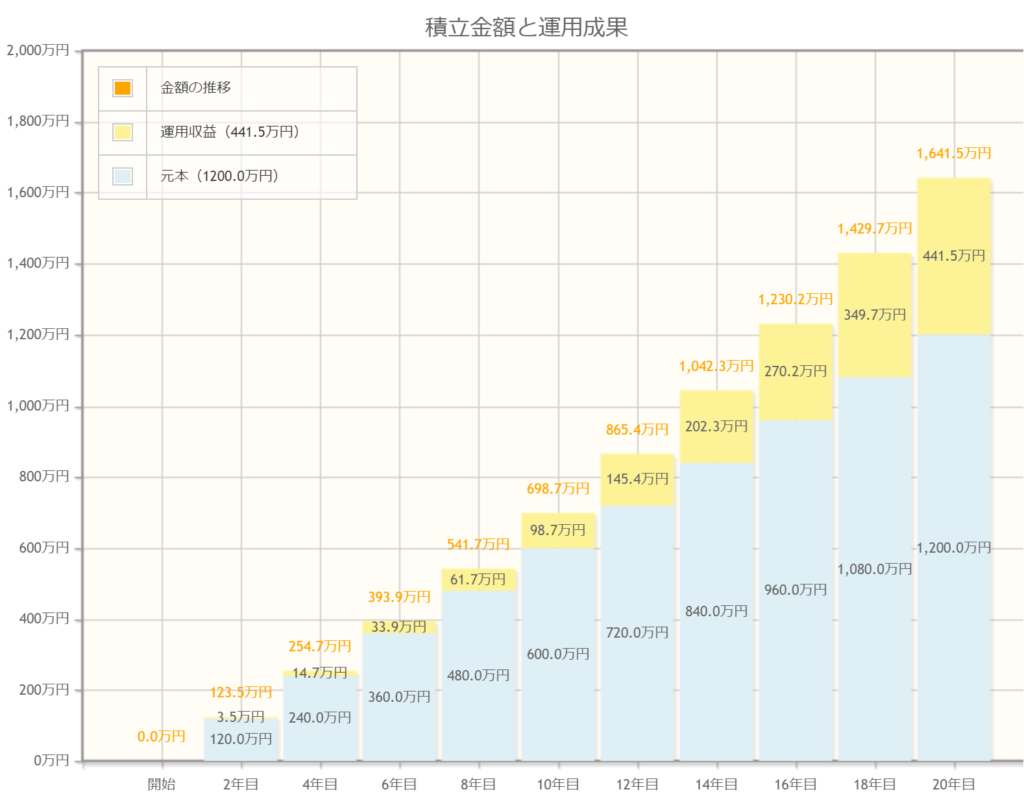
20年運用時点で元本1200万円に対して利益441.5万で計1641.5万となっています。

ちなみに単利式であれば元本1200万円に対して利益361.5万で計1488.1万

153.4万円の差額になります。

これは積立額月5万円で利率3％でのシミュレーションなので積立額を上げたり、もっと良い利回りで運用すれば差はより開くことになります。

これがアインシュタインをして『人類最大の発明』と言わしめた『複利の力』です。

NISA制度での積立シミュレーションをしてみよう

研修医

自分の積み立て予定で将来いくらになるか知りたいですけど計算が出来ません。

Taka

自分でするのは大変なので、『積立シミュレーション』を使ってみて

月にいくら積み立てて何％で運用した額がいくらになるかは自分で計算するのはとても大変です。

先ほどのグラフに使用した金融庁の積み立てシミュレーションが有用です。

他、証券会社でも類似サービスの提供を行っているところがあります。

Taka

国はNISA制度での資産形成を推していますが、背景としては将来年金制度の破綻が考えられるからです。

将来必要な資金を自己で形成するよう促しているんですね。

シミュレーションを使用し、NISA制度での資産形成に役立てていきましょう。

終わりに

今回は『複利』について解説させて頂きました。

Taka

NISA制度を効果的に使用しつつ、『複利』を活かして、将来の資産形成を行っていきましょう。

ここまで読んでいただきありがとうございました。

Taka

医師

Twitter

地方総合病院勤務の20代の消化器内科医師です。インフレが進んでいく社会の中での医師の給料の相対的な低下に危機感を感じて投資・節税等の勉強を始めました。 株式投資歴は5年と浅いですが、資産形成に興味のある方や始めたばかりの方向けの記事を書いていきたいと思います。